Table of Contents
How many symmetry lines are in a trapezoid?
Think of it like a mirror image: if you were to fold an isosceles trapezoid along its line of symmetry, the two halves would perfectly match up. This line of symmetry runs down the middle of the trapezoid, perpendicular to the two parallel sides.
Why do other trapezoids not have a line of symmetry?
Well, if a trapezoid isn’t isosceles, its non-parallel sides are different lengths. This means that if you tried to fold it in half, the two halves wouldn’t match up perfectly.
Let’s break down why this happens. The line of symmetry is defined as a line that divides a shape into two identical mirror images. In an isosceles trapezoid, the line of symmetry is the perpendicular bisector of both the base and the top. This line also divides the trapezoid into two congruent triangles, ensuring that the two halves are identical.
However, in a non-isosceles trapezoid, the non-parallel sides are unequal, which means that the line of symmetry cannot divide the shape into two congruent triangles. Therefore, it cannot be considered a line of symmetry.
So, to summarize, a trapezoid only has a line of symmetry if it’s an isosceles trapezoid. This line of symmetry runs down the middle of the trapezoid, perpendicular to the two parallel sides.
How many symmetry lines does a trapezium have?
A trapezium is a quadrilateral with at least one pair of parallel sides.
A general trapezium has no lines of symmetry. Think of it like a tilted rectangle: its two parallel sides are not the same length, and it doesn’t have any mirror-like reflection.
An isosceles trapezium, where the two non-parallel sides are equal, has one line of symmetry. This line passes through the midpoints of the two parallel sides, dividing the trapezium into two identical halves.
Imagine folding an isosceles trapezium along this line. The two halves would perfectly overlap, demonstrating the symmetry.
It’s important to remember that the maximum number of lines of symmetry a trapezium can have is one. This occurs when the trapezium is isosceles.
Can a trapezoid have no lines of symmetry?
A trapezoid is a quadrilateral with at least one pair of parallel sides. A line of symmetry divides a shape into two identical mirror images.
An isosceles trapezoid has two equal sides, which are not the parallel sides. Because of these equal sides, it has one line of symmetry that runs down the middle, perpendicular to the parallel sides.
Let’s break it down further. Think about a trapezoid that isn’t isosceles. Imagine a trapezoid where the non-parallel sides are different lengths. If you try to draw a line down the middle, you’ll see that the two halves don’t match up perfectly. The line doesn’t create mirror images, so it’s not a line of symmetry.
Here’s an example: Imagine a trapezoid where one non-parallel side is much longer than the other. Now, imagine drawing a line straight down the middle. One side of the line will have a much longer non-parallel side than the other side, so they won’t match up.
So, to sum it up: only isosceles trapezoids have lines of symmetry, and they have just one line of symmetry. Other trapezoids don’t have lines of symmetry because their sides are not symmetrical.
Which has 4 lines of symmetry?
Let’s break down why a square has four lines of symmetry:
Horizontal and Vertical Lines: Imagine drawing a line straight across the middle of the square, dividing it in half horizontally. Now, imagine drawing a line straight down the middle, dividing it in half vertically. These two lines are the most obvious lines of symmetry.
Diagonal Lines: A square also has two diagonal lines of symmetry. These lines run from one corner of the square to the opposite corner.
So, a square has four lines of symmetry: two horizontal, two vertical, and two diagonal. You can think of it like this: a square has a lot of ways to be folded in half, and each of those folds creates a line of symmetry!
Are trapezoids always symmetrical?
Trapezoids are quadrilaterals with at least one pair of parallel sides. However, not all trapezoids are symmetrical. A symmetrical trapezoid is one where the two non-parallel sides are congruent, and the two parallel sides are also congruent. This type of trapezoid is known as an isosceles trapezoid.
To understand symmetry in trapezoids better, let’s look at how folding them works. Imagine you fold an isosceles trapezoid in half along its line of symmetry. The two halves will perfectly match up. This means that the two non-parallel sides are equal in length, as are the two parallel sides. In contrast, if you fold a non-isosceles trapezoid in half, the halves won’t match up perfectly.
It’s important to remember that symmetry is about mirroring – it’s about having two halves that are identical in shape and size. While a parallelogram has no lines of symmetry, it does have rotational symmetry. This means that if you rotate a parallelogram 180 degrees, it will look exactly the same as it did before.
How do you know how many lines of symmetry?
Let’s take a hexagon as an example. Since a hexagon has six sides, it also has six lines of symmetry. Imagine drawing lines through the center of the hexagon. You can draw six lines that cut the hexagon into perfectly matching halves, like a mirror image!
Think about it this way: each line of symmetry goes through a vertex (corner) and the center of the hexagon. Since there are six vertices, there are six lines of symmetry.
Here’s a way to visualize it:
1. Center Point: Mark the exact center of your hexagon.
2. Vertex Connection: Draw a straight line from the center point to one of the vertices (corners).
3. Perfect Halves: This line will divide the hexagon into two identical halves that are mirror images of each other.
4. Repeat: You can repeat this process for each of the six vertices, creating six distinct lines of symmetry.
This same principle applies to all regular polygons. So, if you have a pentagon (five sides), you’ll have five lines of symmetry. A triangle (three sides) will have three lines of symmetry, and so on!
What quadrilateral has 4 lines of symmetry?
Let’s break down what makes a square so special:
Lines of Symmetry: Imagine drawing a line straight down the middle of a square, from top to bottom. You’ve just created a line of symmetry. Now, draw another line across the middle, from side to side. You have two lines of symmetry! If you keep going, you can find two more, running diagonally from corner to corner. That’s a total of four lines of symmetry!
Rotational Symmetry: A square also has rotational symmetry. This means that if you rotate a square by 90 degrees, 180 degrees, or 270 degrees, it will look exactly the same as it did before you rotated it. It takes four 90-degree rotations to get the square back to its original position.
Let’s look at a couple of other quadrilaterals and see how they compare:
Rectangle: A rectangle only has two lines of symmetry. These lines run down the middle and across the middle. A rectangle does not have rotational symmetry of order four.
Rhombus: A rhombus has two lines of symmetry, which run diagonally from corner to corner. A rhombus does not have rotational symmetry of order four.
The square is a unique shape because it has both four lines of symmetry and rotational symmetry of order four. This makes it a very balanced and symmetrical shape.
Can a trapezoid never be a rhombus?
A trapezoid has one pair of parallel sides, while a rhombus has two pairs of parallel sides. This is a key difference. Additionally, all sides of a rhombus are equal in length, while only the parallel sides of a trapezoid are necessarily equal.
Think of it this way: imagine a rhombus as a special kind of trapezoid where the non-parallel sides are also parallel.
Can a trapezoid be a rhombus? The answer is no, because a trapezoid by definition has only one pair of parallel sides, and a rhombus requires two pairs. A trapezoid can only be a rhombus if it meets the requirements of a rhombus – having two pairs of parallel sides and all sides being equal.
Here’s an example:
Imagine a rectangle. A rectangle is a special case of a trapezoid because it has one pair of parallel sides. However, a rectangle is not a rhombus because it has four right angles and its sides are not all equal.
The same goes for any trapezoid. Since it only has one pair of parallel sides, it can never meet the requirements of having two pairs of parallel sides and four equal sides, which are essential to being a rhombus.
So, while some trapezoids might have some similarities to rhombuses (like having one pair of parallel sides), they can’t ever be considered rhombuses. They are distinct shapes with different defining characteristics.
Who has no line of symmetry?
Well, think of it this way: A line of symmetry divides a shape into two identical halves that are mirror images of each other. Scalene triangles, parallelograms, and trapeziums don’t have this property.
Let’s break down why:
Scalene triangles have three sides of different lengths. This means that no matter where you draw a line through them, you won’t be able to create two equal halves.
Parallelograms have two pairs of parallel sides, but their opposite angles are not equal. This means you can’t find a line that creates perfect mirror images.
Trapeziums have only one pair of parallel sides. Since the other two sides are not equal, it’s impossible to create a line of symmetry that divides them equally.
Think of it like folding a piece of paper. If you can fold it in half so that the edges match perfectly, you’ve found a line of symmetry! But if the edges don’t match up, then there’s no line of symmetry.
So remember, not all shapes are symmetrical! Some shapes are unique and interesting in their own way.
What shape has 0 lines of symmetry?
Let’s break down what that means. A line of symmetry is an imaginary line that divides a shape into two identical halves. Think about a square. You can draw a line down the middle, or across the middle, and it would perfectly divide the square in half. But if you try to do that with a scalene triangle, you won’t find any line that creates two identical pieces.
The same goes for parallelograms and trapeziums. These shapes might look symmetrical at first glance, but they don’t have a line that can cut them perfectly in half.
It’s fun to play around with different shapes and see if you can find their lines of symmetry. You might be surprised by how many shapes have none at all!
See more here: How Many Symmetry Lines Does A Trapezium Have? | How Many Lines Of Symmetry Does A Trapezoid Have
How many lines of symmetry does a trapezoid have?
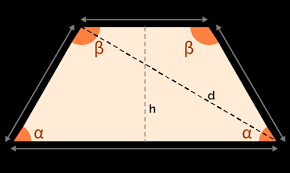
A trapezoid is a four-sided shape with at least one pair of parallel sides. Those parallel sides are called bases, and the non-parallel sides are called legs.
Generally, a trapezoid does not have any lines of symmetry. A line of symmetry is a line that divides a shape into two identical halves. Think of it as a mirror reflecting the shape.
However, there’s a special kind of trapezoid called an isosceles trapezoid that has one line of symmetry.
Why? An isosceles trapezoid has two equal legs and two equal base angles. This symmetry means that you can draw a vertical line down the middle that perfectly splits the shape into two mirror images.
Let’s break down why a regular trapezoid doesn’t have a line of symmetry:
1. Unequal Sides: Most trapezoids have four unequal sides. This lack of equality prevents a line from dividing the shape into identical halves.
2. Unequal Angles: Trapezoids typically have four unequal angles. Imagine trying to fold the trapezoid in half. The angles won’t match up perfectly, making it impossible to find a line of symmetry.
Isosceles trapezoids are different because their equal legs and base angles create a balanced shape. This balance allows for a line of symmetry to exist.
Think of it this way:
* A regular trapezoid is like a lopsided house. It’s difficult to find a point where you can divide it evenly.
* An isosceles trapezoid is like a balanced house. It has equal sides and angles, making it easier to find the center point for a line of symmetry.
So, while most trapezoids lack lines of symmetry, isosceles trapezoids stand out with their singular line of symmetry.
Does an isosceles trapezoid have only one line of symmetry?
Let’s break this down a bit more. Imagine folding an isosceles trapezoid along this line of symmetry. The two halves would perfectly overlap, proving that it’s symmetrical. This is because the line of symmetry divides the trapezoid into two congruent figures—meaning they are exactly the same shape and size.
Think about it this way: if you tried to draw another line of symmetry, you’d run into trouble. If you drew a line perpendicular to the bases, for example, the two halves wouldn’t match up because the non-parallel sides would be different lengths. Similarly, if you drew a line at an angle, you’d have uneven parts on either side of the line.
The key takeaway is that an isosceles trapezoid has just one line of symmetry, and that’s the line that splits it down the middle.
How do you find symmetry on a trapezoid?
Imagine a trapezoid with points labeled A, B, C, and D. Let’s say we have a line of symmetry that divides the trapezoid in half. For the trapezoid to be symmetrical, the distance from point A to the line of symmetry must be equal to the distance from the reflected point, which we can call A’, to the line. This must be true for all points on the trapezoid. For example, the distance from point B to the line of symmetry must equal the distance from point B’ to the line.
Think of it like folding a piece of paper along the line of symmetry. If the trapezoid is symmetrical, the two halves will perfectly match up, with every point on one side having a corresponding point on the other side.
A key thing to remember is that not all trapezoids are symmetrical. Only a special type called an isosceles trapezoid has a line of symmetry. In an isosceles trapezoid, the two non-parallel sides are equal in length, and the line of symmetry runs down the middle, dividing the trapezoid into two congruent triangles.
To find the line of symmetry, you can try drawing a line down the middle of the trapezoid. If you fold the trapezoid along this line and the two halves match up perfectly, then you have found the line of symmetry.
Does a generic trapezoid have reflection symmetry?
Now, an isosceles trapezoid is a different story. This special kind of trapezoid has two equal sides and, most importantly, reflection symmetry. You can draw a line down the middle, connecting the midpoints of the two bases. This line is the line of symmetry and perfectly divides the isosceles trapezoid into two identical halves.
To understand this better, imagine folding an isosceles trapezoid along its line of symmetry. The two halves would perfectly overlap, just like a mirror image. This kind of symmetry is what makes isosceles trapezoids unique and different from other trapezoids.
See more new information: musicbykatie.com
How Many Lines Of Symmetry Does A Trapezoid Have?
Lines of Symmetry and Trapezoids
A line of symmetry is a line that divides a shape into two identical halves. If you could fold the shape along the line of symmetry, both halves would perfectly match. Think about a square. A square has four lines of symmetry because you can fold it in half along any of its diagonals or its midlines.
Types of Trapezoids
There are two main types of trapezoids:
1. Isosceles Trapezoid: This trapezoid has two equal sides, and its non-parallel sides are congruent.
2. Scalene Trapezoid: This trapezoid has no equal sides.
How Many Lines of Symmetry Does a Trapezoid Have?
Now, here’s the deal:
* Isosceles Trapezoid: An isosceles trapezoid has one line of symmetry. This line of symmetry runs vertically down the middle of the trapezoid, dividing it into two congruent halves.
* Scalene Trapezoid: A scalene trapezoid has no lines of symmetry. Since the sides are all different lengths, you can’t fold it in half to create two identical pieces.
Visualizing the Line of Symmetry
Imagine you have an isosceles trapezoid drawn on a piece of paper. If you fold the paper along the middle line of the trapezoid, the two halves will perfectly overlap. That line you folded along is the line of symmetry.
Why is Symmetry Important?
Understanding lines of symmetry isn’t just about shapes and geometry. It’s a concept that shows up in many different fields, from art and design to engineering and architecture.
For example, in art, symmetry is often used to create balance and visual appeal. In architecture, symmetry can help to make buildings more stable and aesthetically pleasing.
FAQs
What is a trapezoid?
A trapezoid is a four-sided polygon (quadrilateral) with at least one pair of parallel sides. The parallel sides are called bases, and the non-parallel sides are called legs.
What is a line of symmetry?
A line of symmetry divides a shape into two identical halves. If you were to fold the shape along the line of symmetry, both halves would perfectly match.
Can a trapezoid have more than one line of symmetry?
No, a trapezoid can have at most one line of symmetry. This only occurs in isosceles trapezoids.
Why doesn’t a scalene trapezoid have a line of symmetry?
A scalene trapezoid doesn’t have a line of symmetry because its sides are all different lengths. You can’t fold it in half to create two identical halves.
What are some real-world examples of trapezoids?
You can find trapezoids all around you. For example:
* Traffic signs: Many traffic signs are shaped like trapezoids.
* Buildings: Some buildings have trapezoid-shaped windows or doors.
* Furniture: Tables and chairs can sometimes have trapezoid-shaped legs or surfaces.
* Objects: You can find trapezoids in everyday objects like cutting boards, cookie cutters, and even some pieces of clothing.
Can a trapezoid be a rectangle?
Yes, a rectangle is a special type of trapezoid where both pairs of opposite sides are parallel and equal in length. It has two lines of symmetry.
Lines of Symmetry – Math Steps, Examples & Questions – Third
Learn about lines of symmetry in 2D shapes, including regular and irregular polygons, circles, and quadrilaterals. Find out how to identify and draw lines of symmetry, and see examples and quizzes for grade 4 math. Third Space Learning
How Many Lines of Symmetry Does a Trapezoid Have
How many lines of symmetry does an isosceles trapezoid have? An isosceles trapezoid has only one line of symmetry. It runs through the midpoints of its parallel sides (bases). Since an isosceles Math Monks
Trapezoid Calculator
Learn how to calculate the area, perimeter, height and angles of a trapezoid with this online tool. A trapezoid has one pair of parallel sides and at least one pair of Omni Calculator
Properties of a Trapezium or Trapezoid (Math Facts)
The main property of a trapezium (as known in Great Britain) or trapezoid (as known in the United States) is that it is a 4-sided shape with exactly one pair of parallel sides. The way in which the trapezium is drawn Owlcation
Q: How many lines of symmetry does a trapezoid have? – CK-12
A generic trapezoid will not have reflection symmetry. An isosceles trapezoid will have reflection symmetry because the line connecting the midpoints of the bases will be a line CK-12 Foundation
Lines of Symmetry – Definition, Examples, and Diagrams – Math
Q2. How many lines of symmetry does the isosceles trapezoid have? Ans. An isosceles trapezoid has 1 line of symmetry, which is the vertical line of symmetry. mathmonks.com
Lines of Symmetry of Plane Shapes – Math is Fun
Learn how to find the lines of symmetry of different shapes by folding them or drawing them. A trapezoid has one line of symmetry, which is parallel to its bases and bisects its non Math is Fun
Trapezoid – Math.net
A trapezoid is a quadrilateral with one pair of parallel sides. An isosceles trapezoid has one line of symmetry: the altitude that bisects its bases. Math.net
Symmetry – Math.net
There are three basic types of symmetry: reflection, rotation, and point symmetry. Reflection symmetry. In Geometry, a figure can have reflection symmetry when it is reflected across a line or a plane. Line symmetry. Math.net
Shapes (Lines Of Symmetry)
How Many Right Angles Can A Trapezoid Have?
Does Every Trapezium Have A Line Of Symmetry?
2021 T2 P1 Q16 Symmetry Properties Of Trapezium
What Does A Trapezoid Look Like ?
How Many Lines Of Symmetry Does A Parallelogram Have
What Are Trapezoids? | Geometry, Quadrilaterals
Line Symmetry And Reflection Symmetry Explained!
Link to this article: how many lines of symmetry does a trapezoid have.
See more articles in the same category here: https://musicbykatie.com/wiki-how/
